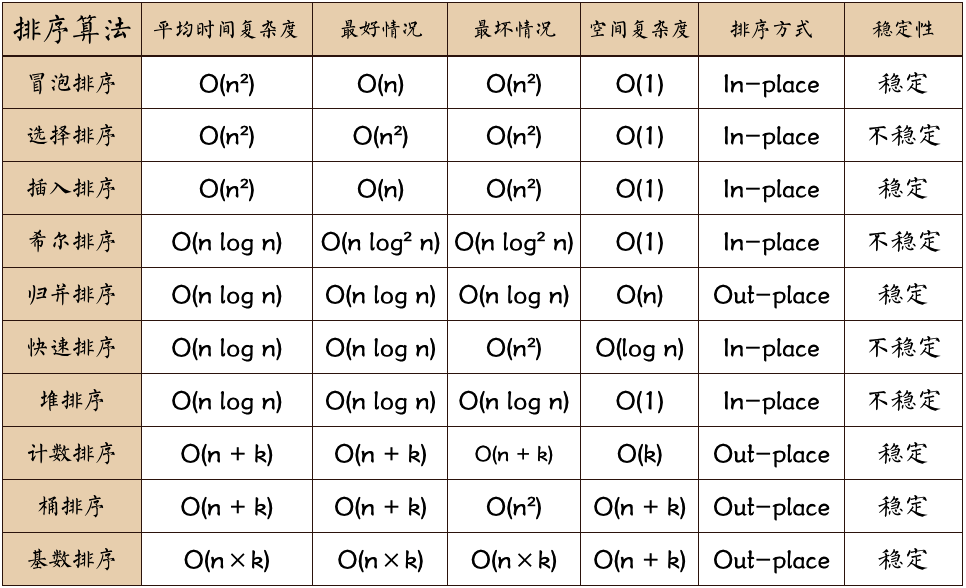
排序算法 整理一些常见的六大基础排序算法: 冒泡排序、选择排序、插入排序 、归并排序 、快速排序 、堆排序
1. 冒泡排序 代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 void BubbleSort (vector<int > &nums) int n = nums.size (); if (n==0 ) return ; for (int i=0 ;i<n;i++) { for (int j=0 ;j<n-1 -i;j++) { if (nums[j] > nums[j+1 ]) { int temp = nums[j]; nums[j] = nums[j+1 ]; nums[j+1 ] = temp; } } }
2. 选择排序
代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 void SelectSort (vector<int > &nums) int n = nums.size (); if (n==0 ) return ; for (int i=0 ;i<n-1 ;i++) { int idx = i; for (int j=i+1 ;j<n;j++) { if (nums[idx] > nums[j]); { idx = j; } if (idx !=i) { int temp = nums[idx]; nums[idx] = nums[i]; nums[i] = temp; } } }
3. 插入排序(重要)
代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 void InsertSort (vector<int > &nums) int n = nums.size (); if (n==0 ) return ; for (int i=1 ;i<n;i++) { int temp = nums[i]; int j = i- 1 ; while (j>=0 ) && (nums[j] > nums[j]) { nums[j+1 ] = nums[j]; j--; } nums[j+1 ] = temp; } }
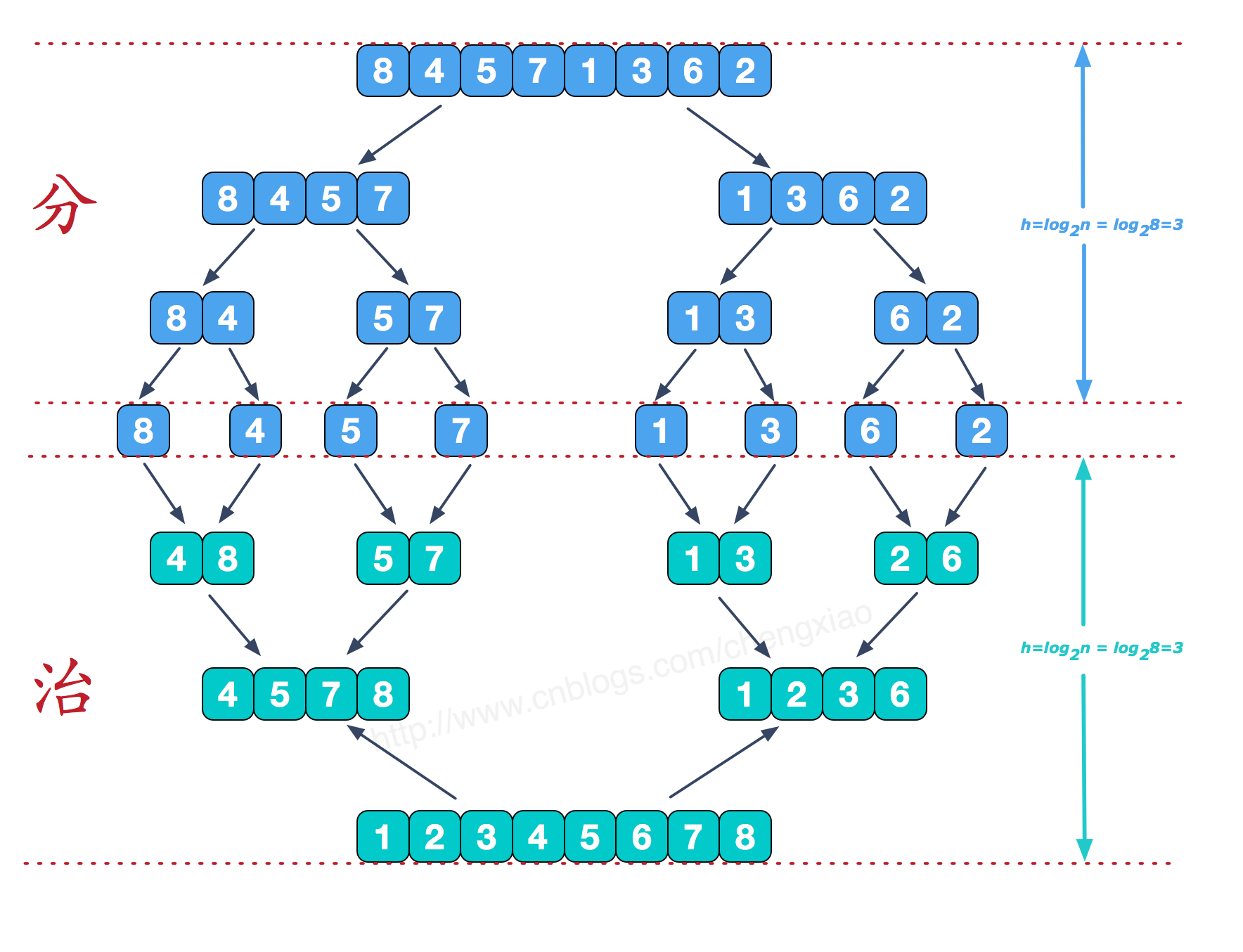
4. 归并排序(重要)
代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 void merge (vector<int > &nums,int low,int high) { int temp[high+1 ]; int mid=(low+high)/2 ; int i=0 ; int l=low; int r=mid+1 ; while (l<=mid&&r<=high) { if (nums[l]<nums[r]) temp[i++]=nums[l++]; else temp[i++]=nums[r++]; } while (l<=mid) { temp[i++]=nums[l++]; } while (r<=high) { temp[i++]=nums[r++]; } i=0 ; while (low<=high) { nums[low++]=temp[i++]; } } void mergesort (vector<int > &nums,int low,int high) { if (low<high) { int mid=(low+high)/2 ; mergesort (nums,low,mid); mergesort (nums,mid+1 ,high); merge (nums,low,high); } }
5. 快速排序(重要)
代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 int Paritition (vector<int > &nums, int low, int high) { int pivot = nums[low]; while (low < high) { while (low < high && nums[high] >= pivot) { --high; } nums[low] = nums[high]; while (low < high && nums[low] < pivot) { ++low; } nums[high] = nums[low]; } nums[low] = pivot; return low; } void QuickSort (vector<int > &nums, int low, int high) { if (low < high) { int i = Paritition (nums, low, high); QuickSort (nums, low, i - 1 ); QuickSort (nums, i + 1 , high); } }
精简版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void QuickSort (vector<int > &nums, int low, int high) if (low < high) { int l = low, r = high, pivot = nums[low]; while (l<r) { while (l<r && nums[r] >=pivot) { r--; } nums[l] = nums[r]; while (l<r && nums[l] < pivot) { l++; } nums[r] = nums[l]; } nums[l] = pivot; quick_sort (nums, low, l-1 ); quick_sort (nums, l+1 , high); } }
6. 堆排序(重要)
代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 void adjustHeap (vector<int > &nums,int i,int length) int temp = nums[i]; for (int k=i*2 +1 ;k<length;k=k*2 +1 ) { if (k+1 <length && nums[k]<nums[k+1 ]) { k++; } if (nums[k] >temp) { nums[i] = nums[k]; i = k; } else { break ; } } nums[i] = temp; } void HeapSort (vector<int > &nums,int n) for (int i=n/2 -1 ;i>=0 ;i--) { adjustHeap (nums,i,n); } for (int j=n-1 ;j>0 ;j--) { swap (nums[0 ],nums[j]); adjustHeap (nums,0 ,j); } }
参考