二分查找算法总结

二分查找法作为一种常见的查找方法，将原本是线性时间提升到了对数时间范围，大大缩短了搜索时间，具有很大的应用场景，而在 LeetCode 中，要运用二分搜索法来解的题目也有很多，但是实际上二分查找法的查找目标有很多种，而且在细节写法也有一些变化。我就对二分查找法的具体写法做个总结。

基础: 二分查找的框架

int binarySearch(vector<int> nums, int target) {
    int start = 0,end = ...;

    while(...) 
    {
        int mid =  start + (end - start) / 2;
        if (nums[mid] == target) 
        {
            ...
        } 
        else if (nums[mid] < target) 
        {
            left = ...
        } 
        else if (nums[mid] > target) 
        {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。

其中 … 标记的部分，就是可能出现细节问题的地方，当你见到一个二分查找的代码时，首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。

另外声明一下，计算 mid 时需要技巧防止溢出，在 start 和 end 都比较大的时候，start + end 很有可能超过 int 类型能表示的最大值，即整型溢出，为了避免这个问题，应该写成： mid=start+(end-start)/2。事实上，int mid = start + (end - start) / 2 在 end 很大、 start 是负数且很小的时候， end - start 也有可能超过 int 类型能表示的最大值，只不过一般情况下 end 和 start 表示的是数组索引值，start 是非负数，因此 end - start 溢出的可能性很小。更好的写法是：int mid = (start + end) >>> 1 .

第一类：寻找一个数（基本的二分查找）

这是最简单的一类，也是我们最开始学二分查找法需要解决的问题,即搜索一个数，如果存在，返回其索引，否则返回 -1，比如我们有数组 [2, 4, 5, 6, 9]，target = 6，那么我们可以写出二分查找法的代码如下：

int binarySearch(vector<int>& nums, int target) {
    if(nums.empty()) return -1;
    int n = nums.size();
    int start = 0;
    int end = n-1;
    while (end>=start)
    {
      int mid = start + (end-start)/2;
      if (nums[mid]==target)
      {
        return mid;
      }
      
      else if (nums[mid]<target)
      {
        start = mid + 1;
      }
      else if (nums[mid]>target)
      {
        end = mid - 1;
      }
    }
    return -1;
}

Q&A:

1.为什么while循环的条件中是 <=，而不是 < ？

答：因为初始化 end 的赋值是 n-1，即最后一个元素的索引，而不是 n。
这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [start, end]，后者相当于左闭右开区间 [start, end)，因为索引大小为 n 是越界的。

我们这个算法中使用的是前者 [start, end] 两端都闭的区间。这个区间其实就是每次进行搜索的区间，我们称之为「搜索区间」。

什么时候应该停止搜索呢？当然，找到了目标值的时候可以终止：

1 2	if(nums[mid] == target) return mid;

但如果没找到，就需要 while 循环终止，然后返回 -1。那 while 循环什么时候应该终止？搜索区间为空的时候应该终止，意味着你没得找了，就等于没找到。

while(start <= end) 的终止条件是 start == end + 1，写成区间的形式就是 [end + 1, end]，或者带个具体的数字进去 [3, 2]，可见这时候搜索区间为空，这时候 while 循环终止是正确的，直接返回 -1 即可。

while(start < end) 的终止条件是 start == end，写成区间的形式就是 [start, end]，或者带个具体的数字进去 [2, 2]，这时候搜索区间非空，还有一个数2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2没有被搜索，如果这时候直接返回 -1 就是错误的。

2.为什么 start = mid + 1，end = mid - 1？我看有的代码是 start = mid 或者 end = mid，没有这些加1减1，如何判断？

答：这也是二分查找的一个难点，刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即 [start, end]。那么当我们发现索引 mid 不是要找的 target 时，如何确定下一步的搜索区间呢？

当然是 [start, mid - 1] 或者 [mid + 1, end] 对不对？因为 mid 已经搜索过，应该从搜索区间中去除。

3.此算法有什么缺陷？

答：至此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但是，这个算法存在局限性。

比如说给你有序数组 nums = [1,2,2,2,3]，target = 2，此算法返回的索引是 2，没错。但是如果我们想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

这样的需求很常见。你也许会说，找到一个 target，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的复杂度了。

我们后续的算法就来讨论这两种二分查找的算法。

第二类：寻找左侧边界的二分搜索

int binarySearch(vector<int>& nums, int target) {
    if(nums.empty()) return -1;
    int n = nums.size();
    int start = 0;
    int end = n;
    while (end>start)  // 搜索区间左闭右开
    {
      int mid = start + (end-start)/2;
      if (nums[mid]==target)
      {
        end = mid;
      }
      else if (nums[mid]<target)
      {
        start = mid + 1;
      }
      else if (nums[mid]>target)
      {
        end = mid;
      }
    }
    // start == n时说明target比所有数都大，不存在返回-1
    // if (nums[start]!=target || start == n) return -1;
    // 返回start是返回的数组中的坐标，就是小于某个数的坐标
    return start;
}

Q&A:

1.为什么 while(start < end) 而不是 <=?

答：用相同的方法分析，因为 end = n 而不是 n - 1 。因此每次循环的「搜索区间」是 [start, end) 左闭右开。
while(start < end) 终止的条件是 start == end，此时搜索区间 [start, start)或者写成[end, end)为空，所以可以正确终止。

2.如何理解左侧边界？

答：

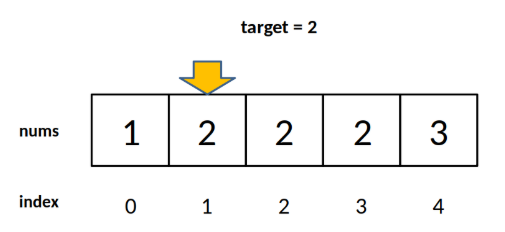
对于这个数组，算法会返回 1。这个 1 的含义可以这样解读：nums 中小于 2的元素有 1 个。

比如对于有序数组 nums = [2,3,5,7], target = 1，算法会返回 0，含义是：nums 中小于 1 的元素有 0 个。

再比如说 nums 不变，target = 8，算法会返回 4，含义是：nums 中小于 8 的元素有 4 个。

综上可以看出，函数的返回值（即 start 变量的值）取值区间是闭区间 [0, n]，如果start的值为n或者nums[start]!=target说明数组中没有目标值，返回-1

3.为什么 start = mid + 1，end = mid ？和之前的算法不一样？

答：这个很好解释，因为我们的「搜索区间」是 [start, end) 左闭右开，所以当 nums[mid] 被检测之后，下一步的搜索区间应该去掉 mid 分割成两个区间，即 [start, mid) 或 [mid + 1, end)。

4.为什么该算法能够搜索左侧边界？

答:关键在于对于 nums[mid] == target 这种情况的处理：

1 2	if (nums[mid] == target) end = mid;

可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 end，在区间 [start, end) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

5.为什么返回 start 而不是 end？

答：都是一样的，因为 while 终止的条件是 start == end。

第三类：寻找右侧边界的二分查找

寻找右侧边界和寻找左侧边界的代码差不多，只有两处不同，已标注：

int binarySearch(vector<int>& nums, int target) {
    if(nums.empty()) return -1;
    int n = nums.size();
    int start = 0;
    int end = n;
    while (end>start)  // 搜索区间左开右闭
    {
      int mid = start + (end-start)/2;
      if (nums[mid]==target)
      {
        start = mid + 1;  // 注意 增大左边界，向右收缩
      }
      else if (nums[mid]<target)
      {
        start = mid + 1;
      }
      else if (nums[mid]>target)
      {
        end = mid;
      }
    }
    return end-1;  //注意
}

Q&A:

为什么这个算法能够找到右侧边界？

答：类似地，关键点还是这里：

1 2	if (nums[mid]==target) start = mid + 1;

当 nums[mid] == target 时，不要立即返回，而是增大「搜索区间」的下界 start，使得区间不断向右收缩，达到锁定右侧边界的目的。

2.为什么最后返回 end - 1 而不像左侧边界的函数，返回 start？而且我觉得这里既然是搜索右侧边界，应该返回 end 才对。

答：首先，while 循环的终止条件是 start == end，所以 start 和 end 是一样的，要体现右侧的特点，返回 end - 1 好了。

至于为什么要减一，这是搜索右侧边界的一个特殊点，关键在这个条件判断：

1 2	if(nums[mid]==target) start = mid + 1;//等价于：mid = start - 1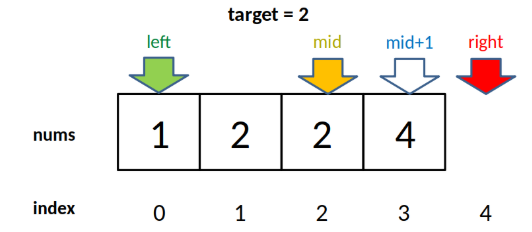

因为我们对 start 的更新必须是 start = mid + 1，就是说 while 循环结束时，nums[start] 一定不等于 target 了，而 nums[start-1] 可能是 target,也就是return end-1。

总结：

来梳理一下这些细节差异的因果逻辑：

第一个，最基本的二分查找算法：

因为我们初始化 end = nums.size() - 1
所以决定了我们的「搜索区间」是 [start, end]
所以决定了 while (start <= end)
同时也决定了 start = mid+1 和 end = mid-1

因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

因为我们初始化 end = nums.size()
所以决定了我们的「搜索区间」是 [start, end)
所以决定了 while (start < end)
同时也决定了 start = mid + 1 和 end = mid

因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

因为我们初始化 end = nums.size()
所以决定了我们的「搜索区间」是 (start, end]
所以决定了 while (start < end)
同时也决定了 start = mid + 1 和 end = mid

因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界

又因为收紧左侧边界时必须 start = mid + 1
所以最后无论返回 start 还是 end，必须减一