2020Fintech
记录一下参加2020招商银行Fintech训练营的初赛题目。
金币
题目
小招在玩一款游戏:在一个N层高的金字塔上,以金字塔顶为第一层,第i层有i个落点,每个落点有若干枚金币,在落点可以跳向左斜向下或向右斜向下的落点。
若知道金字塔的层数N及每层的金币数量分布,请计算小招在本次游戏中可以获得的最多金币数量。
输入描述:1
输入共有N + 1行(N ≤ 1024),第一行为高度N,第二行至N + 1行 ,为该金字塔的金币数量分布。
输出描述:1
输出金币数量。
示例1:1
2
3
4
5
6
7输入:
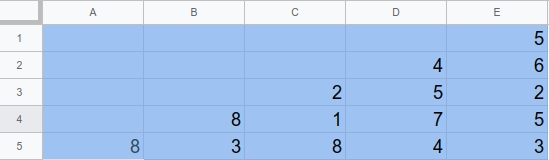
5
8
3 8
8 1 0
4 7 5 4
3 5 2 6 51
2输出:
31
题意概述
相当于给定一个三角形,找出自顶向下的最大路径和。每一步只能移动到下一行中相邻的结点上。
思路
dp
1、定义状态:dp[i][j] 表示从上到下到达 i, j 的最大路径和
2、状态转移方程
到达[i,j]这个位置有两种方法:
从[i-1,j]位置到达
从[i-1,j-1]位置到达
例如:到达coins[3][2],也就是5这个点,只能从coins[2][2],coins[2][1]这两个点
所以很容易写出状态转移方程:
对于首元素与尾元素分别只与一个元素相邻,所以要特殊处理
3、初始状态:
dp[0][0] = coins[0][0]
4、返回结果:
最后一行中最大的dp[i-1][j] (0< j < n)
代码
dp自顶向下,空间复杂度O(n^2)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
using namespace std;
int test(vector<vector<int>>& coins) {
int n = coins.size();
if (coins.empty()) return 0;
if (n==1) return coins[0][0];
int res = 0;
// 定义状态dp[i][j]表示从上到下到达 i, j 的最大路径和
vector<vector<int>> dp(n,vector<int>(n,0));
// 初始状态
dp[0][0] = coins[0][0];
// 状态转移方程
for (int i =1;i<n;i++)
{
// 首行与尾行分别只与一个元素相邻
dp[i][0] = dp[i-1][0] + coins[i][0];
dp[i][i] = dp[i-1][i-1] + coins[i][i];s
for (int j=1;j<i;j++)
{
dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + coins[i][j];
}
}
// 结果为最后一行中最大的
res = dp[n-1][0];
for (int j=0;j<n;j++)
{
res = max(res, dp[n-1][j]);
}
return res;
}
int main()
{
int n;
cin >> n;
vector<vector<int>> coins(n);
for (int i=0;i<n;i++)
{
vector<int> temp(i+1);
for (int j=0;j<i+1;j++)
{
cin >> temp[j];
}
coins[i]= temp;
}
int res = 0;
res = test(coins);
cout << res << endl;
return 0;
}
优化:dp时候每次只用到上一层数据,如果我们倒着,自底向上可以优化成O(n)空间的

此时把行省略,dp设置成1维的,因为每个值只依赖当前值和它右侧的一个值(因为自顶向下是与当前值与当前值左边有关,自底向上反过来),这样从左到右遍历的时候,就可以覆盖上一次的值了,不会影响最后结果。
1 | int test(vector<vector<int>>&coins) |
交换座位
题目
在一场集体婚礼上,有n对新人需要坐在连续排列的 2n个座位上合影,同一对新人彼此挨着。由于进场时各对新人并未按序入座,请计算最少交换座位的次数,以便使每对新人均可并肩坐在一起。一次交换可选择任意两人,让他们互换座位。
全部新人的序号可用 0 到 2n-1 的整数表示,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2n-2, 2n-1)。
row[i]指最初坐在第 i 个座位上的新人编号,i是从0到(2n-1)的一个升序全排列,row不存在重复值。
输入描述:1
输入共有2行,第一行为n,即共有多少对新人(2≤n≤100000 ),第二行为row,即2n个座位上的初始新人编号。
输出描述:1
输出最少交换座位的次数。
示例1:1
2
3输入:
2
0 2 1 31
2输出:
1
说明:1
我们只需要交换1和2的位置即可
示例2:1
2
3输入:
2
3 2 0 11
2输出:
0
说明:1
无需交换座位,所有的新人都已经并肩坐在一起
思路
贪心法:
假设husband的编号为 x,那么wife的编号为 x ^ 1, ^ 在这里是异或操作。对于每张沙发上的第一个人 x = row[i],找到他的同伴,idx = pos[wife]所在的位置 row[idx],将 row[idx] 和 row[i + 1] 互相交换。pos为最初的位置映射。
代码
1 |
|
修塔游戏
题目
小招正在玩一款修塔游戏:系统中有n座高塔,每座高塔由若干个高度相同的方块堆砌而成。修塔游戏的规则为:
(1)每次从最高塔的塔尖拿走一个方块
(2)每次在最低塔的塔尖堆砌一个方块
小招每次只能完成上述两个动作中的一个动作。游戏的目标是使n座高塔中至少有k座高塔的高度相同,请问小招最少需要多少次才能完成游戏。
输入描述:1
输入共有2行,第一行为n和k(1≤k≤n≤200000 ),第二行为n座塔的高度组成的数组 a1, a2, ...an(1≤aj≤10000)。
输出描述:1
输出值为最少需要多少次动作才能完成游戏。
示例1:1
2
3输入:
6 5
1 2 2 4 2 31
2输出:
3
思路
思路主要是:贪心的思想
遍历所有塔的高度作为基准高度,将数组排序,考虑只增高,先増后减,只减,先减后增的情况
代码
1 |
|
