经常会用到栈和队列,也是比较常问到的一个问题,就系统整理一下。
栈(Stack)和队列(Queue)是两种操作受限的线性表。
(线性表:线性表是一种线性结构,它是一个含有n≥0个结点的有限序列,同一个线性表中的数据元素数据类型相同并且满足“一对一”的逻辑关系。
“一对一”的逻辑关系指的是对于其中的结点,有且仅有一个开始结点没有前驱但有一个后继结点,有且仅有一个终端结点没有后继但有一个前驱结点,其它的结点都有且仅有一个前驱和一个后继结点。)
这种受限表现在:栈的插入和删除操作只允许在表的尾端进行(在栈中成为“栈顶”),满足“先进后出”原则;队列只允许在表尾插入数据元素,在表头删除数据元素,满足“先进先出”原则。
栈与队列的相同点:
都是线性结构。
插入操作都是限定在表尾进行。
都可以通过顺序结构和链式结构实现。
插入与删除的时间复杂度都是O(1),在空间复杂度上两者也一样。
栈与队列的不同点:
删除数据元素的位置不同,栈的删除操作在表尾进行,队列的删除操作在表头进行。
应用场景不同;常见栈的应用场景包括括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括计算机系统中各种资源的管理,消息缓冲器的管理和广度优先搜索遍历等。
顺序栈能够实现多栈空间共享,而顺序队列不能。
STL中stack和queue的实现
queue和stack的实现都是默认以deque为底层实现的,这是他们两个的一个相同点
1 | template < class T, class Container = deque<T> > class queue; |
上边说到的不同应用场景不同,这里稍微详细展开说一下
栈的应用:
1.括号匹配问题
判断是否是有效括号(LeetCode 20题有效括号)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
bool isValid(string s) {
stack<char> stk;
int n = s.size();
if (n%2 != 0) return false;
for (int i = 0; i < n; i++)
{
if (s[i] == '(' || s[i] == '[' || s[i] == '{')
{
stk.push(s[i]);
}
else
{
if (stk.empty()) return false;
if (s[i] == ')' && stk.top() != '(') return false;
if (s[i] == ']' && stk.top() != '[') return false;
if (s[i] == '}' && stk.top() != '{') return false;
stk.pop();
}
}
return stk.empty();
}
};
2.十进制表示N进制
十进制表示N进制的话,将十进制对N取余的结果保存在栈中,按序输出栈即可。
1 |
|
3.表达式求值
例如:要计算 2 + 9 / 3 - 5
- 运算数,如:2,9,3等
- 运算符号,如+,-等,而且不同运算符号优先级不一样
由于运算符号优先级不同,而且运算符号位于运算数中,所以使得运算变得复杂了。使用逆波兰算法可以轻松解决。他的核心思想是将普通的中缀表达式转换为后缀表达式。
转换为后缀表达式的好处是:
去除原来表达式中的括号,因为括号只指示运算顺序,不是完成计算必须的元素。
使得运算顺序有规律可寻,计算机能编写出代码完成计算。虽然后缀表达式不利于人阅读,但利于计算机处理。
- 中缀表达式:2 + 9 / 3 - 5
- 后缀表达式:2 9 3 / + 5 -
后缀表达式求值
由于后缀表达式不需要考虑运算符的优先规则,因此求值算法就变得简单了:
从左到右依次遍历表达式;
遇到数字就直接入栈;
- 遇到操作符就弹出两个元素,先弹出的元素放到操作符的右边,后弹出的元素放到操作符的左边(左边的运算数先入栈,因此后出),将计算得到的结果再压入栈;
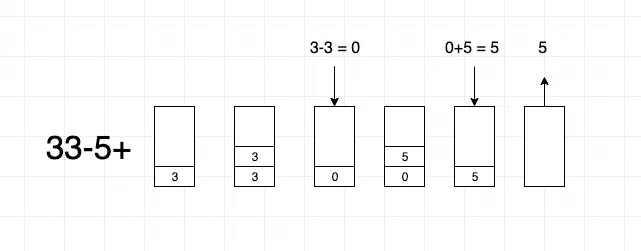
- 直到整个表达式遍历完,最后弹出的栈顶元素就是表达式最终的值。
以33-5+表达式为例,运行状态如下:
LeetCode 150题逆波兰表达式求值1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> s;
int i=0,res;
int n = tokens.size();
while(i<n){
if(tokens[i]=="+"||tokens[i]=="-"||tokens[i]=="*"||tokens[i]=="/"){
int a=s.top();
s.pop();
int b=s.top();
s.pop();
if(tokens[i]=="+"){
res=a+b;
}
else if(tokens[i]=="-"){
res=b-a;
}
else if(tokens[i]=="*"){
res=a*b;
}
else{
res=b/a;
}
s.push(res);
}
else{
int tmp = stoi(tokens[i]);
s.push(tmp);
}
i++;
}
res=s.top();
return res;
}
};
队列的应用
1、生产者消费者模型
2、消息队列
3、排队现象
4、网络数据传输
