KMP字符串

KMP是什么，做什么用的

KMP全称为Knuth Morris Pratt算法，三个单词分别是三个作者的名字。KMP是一种高效的字符串匹配算法，用来在主字符串中查找模式字符串的位置(比如在“hello,world”主串中查找“world”模式串的位置)。

KMP算法的高效体现在哪

高效性是通过和其他字符串搜索算法对比得到的，在这里拿BF(Brute Force)算法做一下对比。BF算法是一种最朴素的暴力搜索算法。它的思想是在主串的[0, n-m]区间内依次截取长度为m的子串，看子串是否和模式串一样(n是主串的长度，m是子串的长度)。代码是这样:

int bf(string main, string pattern) {
    if (main.size() == 0 || pattern.size() == 0 || main.size() < pattern.size()) {
        return -1;  // 异常判断，若不存在返回-1
    }
    int n = main.size();
    int m = pattern.size();
    for (int i = 0; i <= n-m; i++) {
        string s = main.substr(i, m)  // s = main[i : i+m] 截出主串中的对比串
        if (s == pattern) {
            return i; //返回索引值
        }
    }
    return -1; // 主串中不存在模式串
}

BF的时间复杂度是O(N*N)，存在很大优化空间。当模式串和主串匹配时，遇到模式串中某个字符不能匹配的情况，对于模式串中已经匹配过的那些字符，如果我们能找到一些规律，将模式串多往后移动几位，而不是像BF算法一样，每次把模式串移动一位，就可以提高算法的效率。比如说在“ababaababacd”中查找“ababac”，可以避免一些字符之间的比较。

下面通过一个具体的例子来看看可以跳过的情况。比如主模式串是”ababaeaba”,模式串是”ababacd”,在BF算法中，遇到不匹配的情况是这样处理的:

1
2
3

main:    "ababaeaba" // 例如这两个串，当sub为"ababaea"时和"ababacd"进行对比
pattern: "ababacd"   // ，当main[i]为e时，发现和pattern[j]的值e不一致
//BF的做法是去下一个sub,即用"babaeab"和pattern进行比较。

我们希望找到一些规律，遇到两个字符不匹配的情况时，希望可以多跳几个字符，减少比较次数。KMP算法的思想是：在模式串和主串匹配过程中，当遇到不匹配的字符时，对于主串和模式串中已对比过相同的前缀字符串，找到长度最长的相等前缀串，从而将模式串一次性滑动多位，并省略一些比较过程。在上个例子，KMP算法中，是这样处理的：

main:    "ababaeaba" // 比如main中的"ababa"子串，对标为[2~4]的"aba"和pattern中下
pattern: "ababacd"   // 标为[0~2]的"aba"相同,此时可以滑动j-k位,即j=j-k。(其中j是
                                         // pattern中"c"的下标,k是"aba"的长度)。
            "ababaeaba"      // 比较过程中，main[5]为"e"和pattern[5]为"c"不匹配，但是两个
            "ababacd"            // 串中都有相同的"aba"前缀,所以可以滑动j-k位
                    |           
                    ∨
            "ababaeaba"   
                "ababacd"
                    |               // 滑动j-k位后发现main[5]和patterb[3]不相同，需要再次滑动
                    ∨
            "ababaeaba"   
                    "ababacd" // 滑动过程和上次类似。

如何KMP算法的next数组

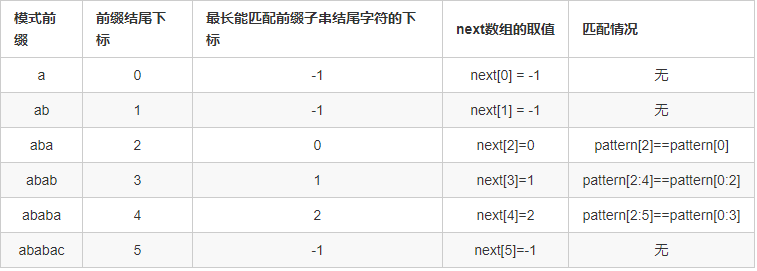
再次明确next数组的含义 : next数组用来存模式串中每个前缀最长的能匹配前缀子串的结尾字符的下标。 next[i] = j 表示下标以i-j为起点，i为终点的后缀和下标以0为起点，j为终点的前缀相等，且此字符串的长度最长。用符号表示为p[0~j] == p[i-j~i]。下面以”ababacd”模式串为例，给出这个串的next数组

KMP的代码

下面给出KMP算法的完整代码，里面有详细的注释。代码从下标1开始。

int kmp(string s, string pattern) {
    int n = s.size();
    int m = pattern.size();
    if (n < m) {
        return;
    }

    // 把next数组中全部初始化为-1
    vector<int> next(m, -1);
    //求next数组中的值
    for (int i = 1, j = 0; i < m - 1; i++ ) {// i从1开始,因为第一个字符如果比较失败了,需重新开始匹配 // i取不到m-1的值, 因为取到m-1意味着整个字符串都相等
        j = next[i-1];  // 前i-1的值是之前循环中比较过的,这里j初始化为next[i-1]

        while (j != -1 && pattern[i] != pattern[j+1]) { // 因为这里是pattern[i]和pattern[j+1]进行比较
            j = next[j]; // 所以这里j是退回到next[j]的位置再进行循环比较
        }

        if (pattern[j+1] == pattern[i]) {  //因为每次循环只会新增一个字符,所以这里用if判断一个新字母即可.
            j++;   // 如果相等则j++
        }

        next[i] = j; // 当前的取值
    } 
    // 匹配的过程
    for (int i = 0, j = 0; i < n; i++) { //模式串从0下标开始匹配
        while(j > 0 && s[i] != pattern[j]) {
            j = next[j-1] + 1; // pattern[j]和s[i]不一致,说明前next[j-1]是匹配的,所以移动next[j-1]位;因为s[i]要继续和pattern[j]进行比较,所以j还需加1
        }
        if (s[i] == pattern[j]) j++;
        if ( j == m-1) return i - m + 1;  //因为j从下标0开始,所以m需减1,两者相等说明循环了len(m)次
    }
    return -1;
}